Correlation Coefficients

When we are interested in determining if there is a relationship between two variables, we determine the correlation. In this course, we will use one of three different correlation coefficients. If our variables are both continuous (interval/ratio) then we will use the Pearson product-moment correlation (r). If one of our variables is ordinal and the other is ordinal, interval, or ratio, then we will use Spearman’s rho (\(r_s\)). If the variables are nominal, we will use the chi-squared test (\(\chi2\)).

Data Visualization

When thinking about correlations, two assumptions that we will consider are linearity and normality. Linearity means that the relationship between the two variables is linear. Normality means that the bivariate relationship is normally distributed. We can observe both using a scatterplot with marginal histograms. We can use the {WVPlots} package to easily graph this visualization.

WVPlots::ScatterHist(dat, xvar = "speed", yvar = "weight",
                     title = "Football Player's Speed and Weight",
                     estimate_sig = TRUE,
                     contour = TRUE)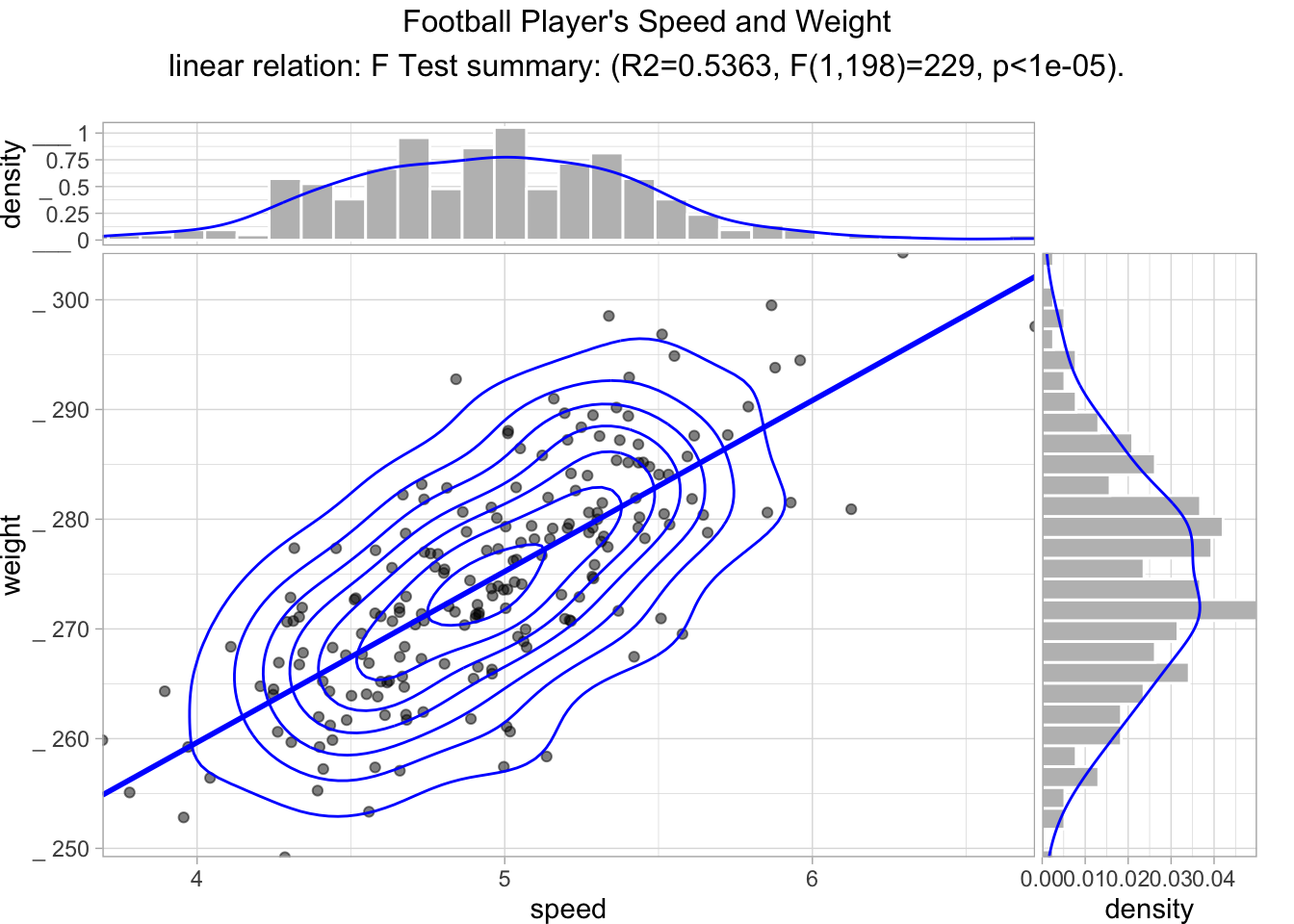

In this visualization, we see that both variables (speed and weight) are generally normally distributed with a bivariate normal distribution. Additionally, we see a linear (vs quadratic) relationship in these data. The correlation of these variables is actually \(r(198) = .73, p = <.001\)

Pearson product-moment correlation.

The Pearson product-moment correlation is used when determining the correlation between two continuous (interval/ration) variables. For example, let’s say a researcher wanted to know if there was a relationship between the amount of sleep a Cadet gets at night and the score on a WPR. We would use the Pearson product-moment correlation. To calculate the Pearson correlation coefficient, we use the cor.test() function and set the method to “pearson.”

cor.test(dat$sleep,
         dat$WPR_score,
         method = "pearson")

## 
##  Pearson's product-moment correlation
## 
## data:  dat$sleep and dat$WPR_score
## t = 10.191, df = 148, p-value < 2.2e-16
## alternative hypothesis: true correlation is not equal to 0
## 95 percent confidence interval:
##  0.5371822 0.7275474
## sample estimates:
##       cor 
## 0.6421603

From these results, we can conclude:

We used a pearson product-moment correlation to determine if there is a relationship between the amount of sleep a Cadet gets at night and their performance on a WPR. The analysis suggests that there is a significant positive relationship \(r(148) = .64, p <.001\). More specifically, an increase in the amount of sleep is related to higher scores on the WPR.

Spearman rho

The Spearman rho correlation is used when determining the correlation between an ordinal variable and a variable that is either ordinal, interval, or ratio. For example, let’s say a researcher wanted to know if there was a relationship between the type of medals athletes won and the amount of money they earned in product endorsements over the next six months (in thousands of dollars). Data was recorded for 28 athletes. Data for the type of medal won was entered as 0= fourth place or worse, 1 = bronze medal, 2 = silver medal, and 3 = gold medal. We would use the Spearman rho correlation. To calculate the Spearman rho correlation coefficient, we use the cor.test() function and set the method to “spearman.”

cor.test(dat$salary,
         dat$medal,
         method = "spearman")

## Warning in cor.test.default(dat$salary, dat$medal, method = "spearman"): Cannot
## compute exact p-value with ties

## 
##  Spearman's rank correlation rho
## 
## data:  dat$salary and dat$medal
## S = 2389.5, p-value = 0.07124
## alternative hypothesis: true rho is not equal to 0
## sample estimates:
##       rho 
## 0.3460678

From these results, we can conclude:

We used a Spearman rho correlation to determine if there is a relationship between the medal an Olympic athlete received and their Salary over the next six months. The analysis suggests that there is not a significant relationship \(r_s(28) = .35, p = .07\).

Note that the degrees of freedom are not provided from the cor.test() function when using a spearman method. In this case, the degrees of freedom is equal to the number of variable pairs (number of observations of complete data).

Chi-Squared test

The Chi-Squared test is used to either determine correlations between two categorical (nominal) variables (Chi-Squared test for independence) or to determine if a categorical variable follows a hypothesized distribution (Chi-Squared test for goodness of fit).