t-test

When we are interested in determining if there is a difference in a continuous (interval/ratio) dependent variable between two categories in a discrete (typically nominal/ordinal) independent variable, we use a difference in means test, also known as a t-test.

To conduct a t-test within R, we will use the t.test() function from the [stats] package.

the t.test() has several parameters that can be adjusted to match the type of test you are looking to perform.

Types of t-tests

One Sample t-test:

A one sample t-test is used to compare means of a sample to a known population mean.

The input for this is one vector of data and mu will be the population parameter you are comparing against.

Paired Samples t-test:

A paired samples t-test is used to compare the means of two paired samples. This is common with before and after samples where the same participants are used at both measurement time points.

The input for this is two vectors of data (one one vector and a grouping parameter). The paired parameter within the t.test() will be set to TRUE.

Independent Samples t-test:

An independent samples t-test is used to compare the means of two independent samples. This is more common when we are comparing groups at one time point (e.g., difference in means of some variable according to sex assigned at birth).

the input for this is the two vectors of data (or one vector and a grouping parameter). The paired parameter within the t.test() will be set to FALSE.

Student t-test:

The Student t-test is used when the data are normally distributed and the variances between the groups are equal.

The var.equal parameter within the t.test() will be set to TRUE.

Welch t-test:

The Welch t-test is used to compare means of two samples when the variances between the two groups are not equal. The Welch t-test still assumes normality of the data.

The var.equal parameter within the t.test() will be set to FALSE.

Wilcoxon rank test:

The Wilcoxon rank test is a non-parametric test to compare medians of two samples that are not normally distributed.

We will use the wilcox.test() function from the [stats] package to conduct this non-parametric test.

Assumptions:

The data must be normally distributed. This can be tested using a Shapiro-Wilkes test for normality. If normality cannot be established, it is recommended to use a non-parametric test such as the Wilcoxon rank test.
The variances between the two groups (independent samples t-test) must be equal. This can be tested using a Levene test (also called an F-Test). If the variances are not equal, it is recommended to use a Welch t-test.

Process:

Creating some data to use:

We’ll create a dataset with three columns. The first particpant will be a participant ID number. The second variable will be height which is the height of the participant. The third variable is sex which is the sex assigned at birth for the participant.

set.seed(63)
dat <- data.frame(
  participant = paste0(rep("P_", 20), 1:20),
  height = round(rnorm(20, c(64, 69), c(2, 3)), 1),
  sex = rep(c("female", "male"), times = 10)
)

Now we will walk through an example.

Step 1: Determine your research question.

The first step is to determine what you want to compare. For this example, we want to see if there is a difference in height between men and women in our sample. This is clearly an independent samples t-test.

Step 2: Visualize these data

The first thing we want to do is see these data. A boxplot works well for this type of visualization. If you have a lot of data points, a raincloud plot may be a better option.

dat %>% 
  ggplot(aes(x = sex, y = height)) + 
  geom_boxplot()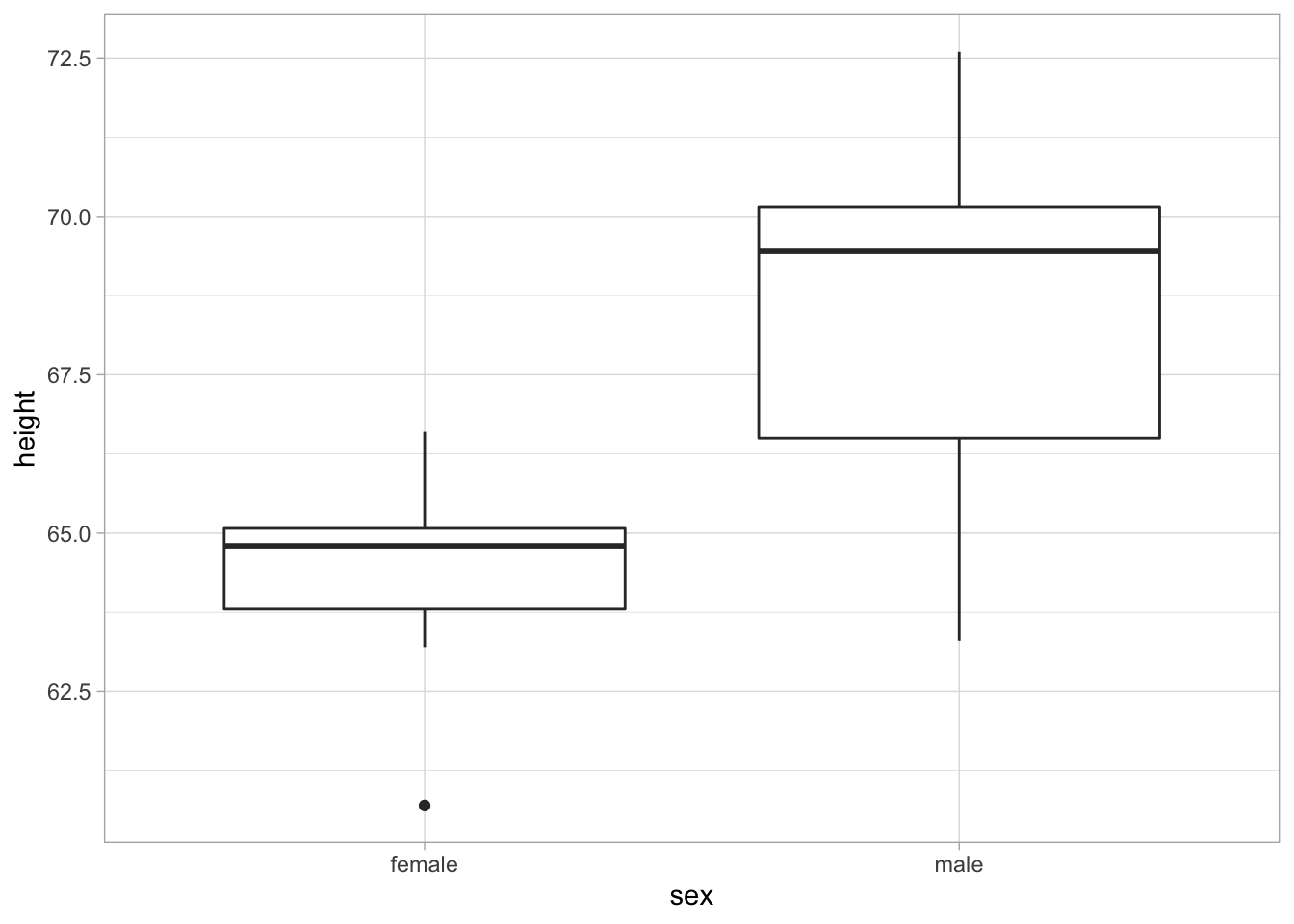

it seems that we may have a difference between the mean height of the women in our study and the mean height of the men in our study. The variances also appear to be a bit different. Something we will need to test going forward.

Step 3: Test assumptions

Normality: To test for normality, we will use a Shapiro-Wilkes test.

women <- dat %>% filter(sex == "female") %>% pluck("height") %>% shapiro.test(.)
women

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.89163, p-value = 0.1769

With reference to the women in the study, the p-value of the Shapiro-Wilkes normality test (\(p\) = 0.177) is not significant indicating that the distribution is not significanlty different than normal (our null hypothesis).

men <- dat %>% filter(sex == "male") %>% pluck("height") %>% shapiro.test(.)
men

## 
##  Shapiro-Wilk normality test
## 
## data:  .
## W = 0.89601, p-value = 0.198

With reference to the men in the study, the p-value of the Shapiro-Wilkes normality test (\(p\) = 0.198) is not significant indicating that the distribution is not significanlty different than normal (our null hypothesis).

Equality of Variance We test whether the variances are the same using the F-Test.

res.ftest <- var.test(height ~ sex, data = dat)
res.ftest

## 
##  F test to compare two variances
## 
## data:  height by sex
## F = 0.25875, num df = 9, denom df = 9, p-value = 0.05663
## alternative hypothesis: true ratio of variances is not equal to 1
## 95 percent confidence interval:
##  0.06426889 1.04171060
## sample estimates:
## ratio of variances 
##          0.2587462

When comparing the two variances, we see that the ratio of variances is not significantly different from 1 (F (9, 9) = 0.259, \(p\) = 0.057).

Step 4: Conduct the t-test

We have satisfied the assumptions needed to conduct a Student two-sample t-test and will use this to determine whether a mean difference exists between the height of men and the height of women in our study.

res.ttest <- t.test(height ~ sex, 
                    data = dat, 
                    mu = 0, # change this to pop. parameter if you are doing a one sample t-test
                    alternative = "two.sided", # you can change this to "less" or "greater"
                    paired = FALSE, # Change this to TRUE if you are doing a paired samples t-test
                    var.equal = TRUE) # Change this to FALSE to use the Welch two sample t-test
res.ttest

## 
##  Two Sample t-test
## 
## data:  height by sex
## t = -3.4915, df = 18, p-value = 0.002605
## alternative hypothesis: true difference in means between group female and group male is not equal to 0
## 95 percent confidence interval:
##  -6.406878 -1.593122
## sample estimates:
## mean in group female   mean in group male 
##                64.43                68.43

When comparing the average height between men and women in our sample, we see that the height of men is significantly different than the height of women (t (18) = -3.492, \(p\) = 0.003).